A mini Mathematica Tutorial

$\fbox{ \parbox{17cm}{ \large{ {\bf A mini Mathematica tutorial} 4/24-25/2001 \hfill {\bf Oliver Knill, knill@math.harvard.edu} } }}$

Integrate[Sin[x]^8,x]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ LOOK UP. To use Mathe... ...ccount. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{shot1/shot1.ps}}} }}$

Plot[x*Sin[1/x],{x,-1,1}]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ 2D PLOT. To plot a fu... ...ac/Unix). } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{plot/plot.ps}}} }}$

Plot3D[Sin[x*y],{x,-3,3},{y,-3,3}];Display["plot3.ps",%,"EPS"]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ 3D PLOT. Plot a funct... ...erminal. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{plot/plot3.ps}}} }}$

Plot3D[Sin[x*y],{x,-3,3},{y,-3,3},PlotPoints->100,Mesh->False,Boxed->False]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ 3D PLOT (II) The same... ...s. etc. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{plot/plot3a.ps}}} }}$

ContourPlot[Sin[x*y],{x,-3,3},{y,-3,3},PlotPoints->200,ColorFunction->Hue]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ CONTOUR PLOTS allow t... ...itude. } \parbox{7.9cm}{\scalebox{0.35}{\includegraphics{plot/contour.ps}}} }}$

S=DSolve[{x''[t]==-x[t],x[0]==1,x'[0]==0},{x},t];Plot[Evaluate[x[t]/.S],{t,0,10}];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ SOLVING DIFFERENTIAL ... ...cillator. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{ode/orbit.ps}}} }}$

S=NDSolve[{x''[t]-0.2*(1-x[t]^2)*x'[t]+x[t]==0,x[0]==1,x'[0]==0},x,{t,0,40}]
T=ParametricPlot[Evaluate[{x[t],x'[t]}/.S[[1]]],{t,0,40}]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ PHASE SPACE PLOT. The... ...ycle. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{ode/vanderpol.ps}}} }}$

Needs["Graphics`PlotField`"]
f[x_,y_]:={x(6-2x-y),y(5-x-y)};PlotVectorField[f[x,y],{x,0,4},{y,0,4}]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ VECTOR FIELDS. When d... ... in space. } \parbox{7.9cm}{\scalebox{0.35}{\includegraphics{ode/phase.ps}}} }}$

M=Compile[{x,y},Block[{z=x+I*y,k=0},While[Abs[z]<2&&k<50,z=z^2+x+I*y;++k];k]];
DensityPlot[50-M[x,y],{x,-2,1},{y,-1.5,1.5},PlotPoints->200,Mesh->False];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ COMPILED FUNCTIONS. C... ...parbox{7.9cm}{\scalebox{0.45}{\includegraphics{mandelbrot/mandelbrot.ps}}} } }$

<<Graphics`Polyhedra`;
F[0]:=Dodecahedron[]; F[n_]:=Stellate[F[n-1]];
Show[Graphics3D[F[2]],Boxed->False]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ POLYHEDRA. Some basic... ... } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{stellate/stellate.ps}}} } }$

Eigenvalues[{{1,1,0,0},{0,1,1,1},{1,3,2,3},{1,2,3,4}}];
ListDensityPlot[Inverse[Table[Random[],{i,1,500},{j,1,500}]]];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ EIGENVALUES. You ofte... ...a. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{inverse/inverse.ps}}} } }$

A=ReadList["d.dat",Number];n=Length[A];B=Table[{i,A[[i]]},{i,n}];
f[u_]:=Fit[B,{1,x,x^2,x^3,x^4},{x}]/.{x->u};Plot[f[u],{u,0,Length[A]}];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ FIT DATA. Want to fit... ...he data. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{data/data.ps}}} } }$

Needs["Graphics`Polyhedra`"]
M[0,{i_,j_,k_}]:={Cuboid[{i,j,k}]};
M[n_,{i_,j_,k_}]:=Module[{s={}},Do[If[Not[u==v==2||v==w==2||u==w==2],
s=Union[s,M[n-1,3^(n-1)*{u,v,w}+{i,j,k}]]],{u,3},{v,3},{w,3}];s];
Show[Graphics3D[M[3,{0,0,0}]],Boxed->False];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ PROGRAMMING. The abov... ...ace. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{menger/menger.ps}}} } }$

Series[Log[1+Sin[x]],{x,0,5}]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ TAYLOR SERIES. Forgot... ...e ... } \parbox{7.9cm}{\scalebox{0.55}{\includegraphics{series/series.ps}}} } }$

n=2^2^7+1;Print[n];FactorInteger[n]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ RSA. Want to factoriz... ...ber. } \parbox{7.9cm}{\scalebox{0.55}{\includegraphics{factor/factor.ps}}} } }$

T[{x_,y_}]:={0.3*y+1-1.4*x^2,x};ListPlot[NestList[T,{.5,.3},10^4]]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ CHAOS. The above Math... ... code. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{henon/henon.ps}}} } }$

Solve[x^3+ax^2+bx*c==0,x]

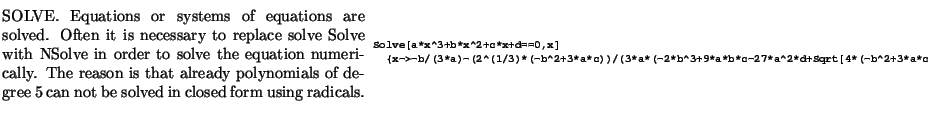
$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ SOLVE. Equations or s... ...icals. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{solve/solve.ps}}} } }$

g={{-(1-2m/r),0,0,0},{0,1/(1-2m/r),0,0},{0,0,r^2,0},{0,0,0,r^2*Sin[theta]^2}};
ginverse=Simplify[Inverse[g]];x={t,r,theta,phi};
h[j_,k_,i_]:=(D[g[[k,i]],x[[j]]]+D[g[[i,j]],x[[k]]]-D[g[[j,k]],x[[i]]])/2;
h=Table[h[j,k,i],{j,4},{k,4},{i,4}];
G[j_,k_,i_]:=Sum[ginverse[[i,l]]*h[[j,k,l]],{l,4}];
G=Table[G[j,k,i],{j,4},{k,4},{i,4}];
Riemann[i_,k_,m_,n_]:=D[G[[k,n,i]],x[[m]]]-D[G[[k,m,i]],x[[n]]]
+Sum[G[[k,n,j]]*G[[j,m,i]]-G[[k,m,j]]*G[[j,n,i]],{j,4}]
Ricci[i_,k_]:=Sum[Riemann[j,i,k,j],{j,4}];
Ricci=Table[Ricci[ii,kk],{ii,4},{kk,4}];Simplify[Ricci]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ SYMBOLIC CALCULATIONS... ... } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{einstein/einstein.ps}}} } }$

s=NDSolve[{D[u[x,t],t]==D[u[x,t],{x,2}],u[x,0]==Sin[5*Pi*x], u[0,t]==0,u[1,t]==0},u,{x,0,1},{t,0,.01}];
S=Plot3D[Evaluate[u[x,t]/.s[[1]]],{t,0,.01},{x,0,1}, PlotPoints->50,PlotRange->{-1,1}];

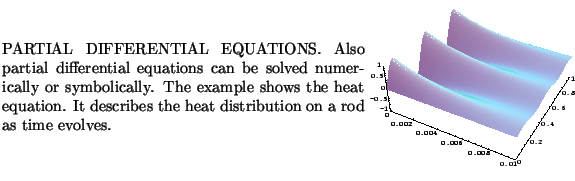
$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ PARTIAL DIFFERENTIAL ... ...evolves. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{heat/heat.ps}}} } }$

s=NDSolve[{D[u[x,t],{t,2}]==D[u[x,t],{x,2}]-20*Sin[x], u[x,0]==Sin[6*Pi*x],
Derivative[0,1][u][x,0]==-6*Pi*Cos[6*Pi*x], u[0,t]==0, u[1,t]==0},u,{x,0,1},{t,0,1}];
Plot3D[Evaluate[u[x,t]/.s[[1]]],{t,0,1},{x,0,1}];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ NONLINEAR WAVE EQUATI... ...blow up. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{wave/wave.ps}}} } }$

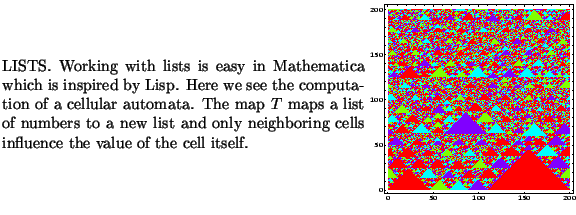
n=5;T[x_]:=Mod[x+RotateRight[x]-RotateLeft[x],n];
U=NestList[T,Table[Floor[n*Sin[k/100]^2],{k,200}],200];
S=ListDensityPlot[U/(n+1),Mesh->False,ColorFunction->Hue];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ LISTS. Working with l... ... } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{cellular/cellular.ps}}} } }$

Needs["Graphics`Graphics`"];
A=ReadList["grades.dat",Number];n=Length[A];{m,M}=Floor[{Min[A],Max[A]}];
Mean=Sum[A[[i]],{i,n}]/n;Var=Sum[(A[[i]]-Mean)^2,{i,n}]/n;StDev=Sqrt[Var];
B=Table[0,{k,M}];Do[B[[A[[i]]]]=B[[A[[i]]]]+1,{i,n}];
S1=BarChart[A];S2=BarChart[B];S3=PieChart[A];S4=PieChart[A,PieExploded->All];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ STATISTICS. Calculati... ...\parbox{7.9cm}{\scalebox{0.45}{\includegraphics{statistics/statistics.ps}}} } }$

Factor[234123142341234]>>file.out
Directory[]
FileNames[]
Run["date"]
<<file.out
DeleteFile["file.out"]

$\textstyle \parbox{16cm}{ FILES. Mathematica can be used as a shell. You can run other programs from within Mathematica, write or read to files. }$

Needs["Graphics`Polyhedra`"]
t=ToCharacterCode; gif[n_]:=FromCharacterCode[Join[t["f"],IntegerDigits[n]+48,t[".gif"]]];
S[n_]:=Show[Stellate[Polyhedron[Icosahedron],6*Sin[2Pi*n/60]^2],Boxed->False];
Do[Display[gif[1000+n],S[n],"GIF"],{n,60}];Run["gifmerge -l0 -10 f*.gif>movie.gif"];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ ANIMATION. Since Math... ...} \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{animation/animation.ps}}} } }$

<<Graphics`Shapes`;
A={{-2Pi,0.0},{-1.0,2Pi}}; S=Transpose[Eigensystem[A][[2]]]; l=Eigensystem[A][[1]];
y[t_]:={-Cos[l[[1]]*t],0.2*Cos[l[[2]]*t]};a[{u_,v_}]:={-(10+20*(u+2)/4),10*v};x[t_]:=a[S.y[t]];
r[h_]:={5,0,h}; R[t_]:={{Cos[t],-Sin[t],0},{Sin[t],Cos[t],0},{0,0,1}};
ball[h_]:={AbsolutePointSize[20],RGBColor[1,0,0],Point[{0,0,h}]}; c=0.8;
rod[h_,theta_]:={AbsolutePointSize[10],Cuboid[R[theta].r[h]-{c,c,c},R[theta].r[h]+{c,c,c}],
Line[{{0,0,h},R[theta].r[h]}]}; cube[h_]:=Cuboid[{-2,2,-0.01},{2,-2,-2}];
spring[h_]:=ParametricPlot3D[{Sin[t],Cos[t],h*t/60},{t,1,60}];
s[h_,theta_]:={spring[h],Graphics3D[{cube[h],ball[h],Table[rod[h,theta+2*k*Pi/5],{k,5}]}]}
T[k_]:=Show[s[x[k/30][[1]],x[k/30][[2]]],AspectRatio->1,DisplayFunction->Identity,
Boxed->False, Axes->False, PlotRange->{{-10,10},{-10,10},{-30,0}}];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ ILLUSTRATION. Instead... ...n. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{spinner/spinner.ps}}} } }$

Zermatt=Import["images/zermatt.ps"];
Display["zermatt.ps",Show[Zermatt],"EPS"];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ GRAPHICS. You can imp... ...nd. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{images/zermatt.ps}}} } }$

<<sound.m
Play[Sin[1000*x]+Cos[2000*x]+Sin[10000*x],{x,0,20}];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ SOUND. Instead of plo... ...sizer. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{sound/sound.ps}}} } }$

Table[Timing[FactorInteger[n!+1]][[1]],{n,1,30}]

$\textstyle \parbox{16cm}{ TIMING. Any calculation can be timed. }$

T1[x_]:=4x(1-x); T2[x_]:=4x-4*x^2; S[n_]:=Last[NestList[T1,0.3,n]-NestList[T2,0.3,n]];

$\textstyle \parbox{16cm}{ PRECISION. For chaotic dynamical systems like the Log... ...ustration that the distributive law is not true for floating point numbers. }$

n=5; R:=Random[]; p=2Pi;V=N[Table[{Cos[p*(k+R/3)/n],Sin[p*(k+R/3)/n]},{k,n}]];
P0={5,2}; NN=10000;lef[{xx_,yy_},l_]:=Module[{},ll=Mod[l-1,n]+1; mm=Mod[l,n]+1;
(V[[mm,2]]-V[[ll,2]])*(xx-V[[ll,1]])<(yy-V[[ll,2]])*(V[[mm,1]]-V[[ll,1]])];
Ex[P_]:=Module[{},Do[If[((!lef[P,j]) && lef[P,j+1]),kk=j],{j,n}];Mod[kk,n]+1];
T[P_]:=Module[{kkk=Ex[P]},2*V[[kkk]]-P];Orbit=NestList[T,P0,NN];
Points=Table[{Hue[k/NN],PointSize[0.001],Point[Orbit[[k]]]},{k,NN}];
Tisch={RGBColor[0,0,1],Polygon[V]}; bg=GrayLevel[0.0];
U=Show[Graphics[{Tisch,Points}],PlotRange->All,AspectRatio->1,Background->bg];
Display["exterior.ps",U,"EPS"]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ EXTERIOR BILLIARDS. W... ... } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{exterior/exterior.ps}}} } }$

tune={0,0,4,4,7,7,5,4,2,2,0,4,7,4,0,0,0,0,0};
scale[n_]:=2000*2^(n/12); beatlength=1/3;
frequency[x_]:=tune[[1+Floor[x/beatlength]]];
hull[x_]:=Sin[x]+Cos[3x]/3+Sin[6x]/5;
f[t_]:=hull[scale[frequency[t]]*t];
Play[f[t],{t,0,5}];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ SOUND. Mathematica us... ...ction. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{sound/sound.ps}}} } }$

<<Graphics`Polyhedra`;
WS[s__]:=WriteString["dodec.inc",s];W[s_]:=Write["dodec.inc",s];
VertexToPovray[L_]:=Module[{},
Do[ WS["#declare P"];W[i];a=N[L[[i,1]],16];b=N[L[[i,2]],16];c=N[L[[i,3]],16];
WS["=<"]; W[a];WS[","]; W[b]; WS[","];W[c];WS[">;"];WS["\n"],{i,Length[L]}]];
FaceToPovray[F_]:=Module[{nf=Length[F[[1]]]},
Do[ WS["face(P"];Do[W[F[[i,j]]]; WS[",P"],{j,nf-1}];
W[F[[i,nf]]]; WS[")"];WS["\n"],{i,Length[F]}]];
VertexToPovray[Vertices[Dodecahedron]];
FaceToPovray[Faces[Dodecahedron]];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ EXPORT TO RAYTRACERS.... ...ring. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{povray/proto.ps}}} } }$

R[{x_,y_}]:=If[Abs[x]+Abs[y]>100,{100,100},{x,y}];T[{x_,y_}]:=R[{g x-x^3-y,x}];
ps=0.001;num=15;len=1000; Orb[p_,n_]:=Module[{t={p},q=p},Do[If[Abs[q[[1]]]>99,
Return[{Hue[Random[]],PointSize[ps],Map[Point,t]}]]; q=T[q];
t=Append[t,q],{j,n}];{Hue[Random[]],PointSize[ps],Map[Point,t]}];
S=Module[{},g=h=2.5; s={};
Do[s=Join[s,Orb[{1.0*k/num,1.0*k/num},len]],{k,-num,num}];
Show[Graphics[s,Axes->False,AspectRatio->1,Background->GrayLevel[0.0],
PlotRange->{{-1.5,1.5},{-1.5,1.5}}]]];Display["henon1.ps",S,"EPS"];

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ CONSERVATIVE MAPS. An... ... map. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{henon/henon1.ps}}} } }$

P=N[Pi];p=6;Coord[{a_,b_}]:={a,Cos[b]}; R=Random;
f[t_,y_,x_]:=-Cos[3t-y]/4-p*Cos[y]+Cos[3*t+y]/2+
Cos[t-4*x+y]/4+p*Cos[t-x+y]-Cos[t+2*x+y]/2;
T[{t_,y_}]:=Module[{},t1=FindRoot[f[t,y,x]==0,{x,t+2y}][[1,2]];
While[(t1-t)^2<10^(-10),t1=FindRoot[f[t,y,x]==0,{x,t+R[]}][[1,2]]];
{Mod[t1,2P],Mod[t1-t-y,P]}];
Orb[a_,b_,n_]:=Module[{u={a,N[ArcCos[b]]}},Do[u=T[u];
s=Append[s,Coord[u]],{j,n}];s];
M[t_]:=-I/2*(1-E^(-2*I*t))-I/4*(-1+E^(4*I*t))-I*(-1+E^(I*t))*p;
Tisch[t_]:={Re[M[t]],Im[M[t]]};ST:=ParametricPlot[Tisch[t],{t,0,2P},
Axes->False,AspectRatio->1,DisplayFunction->Identity];
Trajectory[O_]:=Table[{Thickness[0.0001],Hue[i/Length[O]],
Line[{Tisch[O[[i,1]]],Tisch[O[[i+1,1]]]}]},{i,Length[O]-1}];
ShowTraj[a_,b_,n_]:=Module[{},s={};OOO=Orb[a,b,n];
Show[Graphics[Trajectory[OOO]],DisplayFunction->Identity]];
TT[a_,b_,n_]:=Show[{ShowTraj[a,b,n],ST},
Axes->False,DisplayFunction->$DisplayFunction,AspectRatio->1];
S=Show[GraphicsArray[{{TT[1.0,0.470,200],TT[1.0,0.060,200],
TT[1.0,0.07-0.0006,32]},{TT[1.0,0.07-0.0006,32],
TT[1.0,0.939,200],TT[1.8,0.500,200]}}]];
Display["billiard.ps",S,"EPS"]

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ BILLIARDS. Billiards ... ... } \parbox{7.9cm}{\scalebox{0.55}{\includegraphics{billiard/billiard.ps}}} } }$

http://www.mathematica.com
http://www.mathematica-journal.com
http://www.mathsource.com

$\textstyle \parbox{16cm}{ \parbox{16.0cm}{ \parbox{8.cm}{ RESOURCES. There are ... ...r thing. } \parbox{7.9cm}{\scalebox{0.45}{\includegraphics{luge/luge.ps}}} } }$

http://www.maplesoft.com
http://www.mathworks.com
http://www.maths.usyd.edu.au:8000/u/magma/
http://http://www.octave.org/
http://http://www.math.columbia.edu/~bayer/Macaulay/
http://www.scientificweb.com/software/macsyma/macsymae.html
http://www.mathsoft.com
http://http://www.uni-koeln.de/REDUCE/

$\textstyle \parbox{16cm}{ OTHER COMPUTER ALGEBRA PACKAGES. Besides Mathematica,... ...Reduce (current 3.7): 20 years old. Full source code available. \end{itemize}}$

Oliver Knill
2001-04-23