

Next: Bibliography
Up: The life and works
Previous: Yang-Mills equations over Riemann
Let 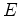 and
and 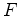 be vector bundles over a compact manifold
be vector bundles over a compact manifold 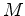 . If a
differential operator
. If a
differential operator
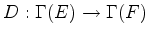 is elliptic, then
is elliptic, then
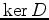 and
and
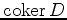 are finite-dimensional vector spaces and we can
define the index of
are finite-dimensional vector spaces and we can
define the index of 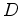 to be the virtual vector space
to be the virtual vector space
Now suppose a Lie group 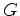 acts on
acts on 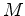 , and
, and 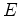 and
and 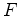 are
are
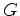 -equivariant vector bundles over
-equivariant vector bundles over 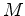 . Then
. Then 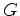 acts on
acts on
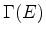 by
by
for 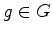 ,
,
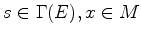 . The
. The 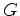 -action is said to
preserve the differential operator
-action is said to
preserve the differential operator 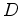 if the actions of
if the actions of 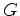 on
on
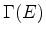 and
and
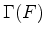 commute with
commute with 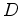 .
In this case
.
In this case 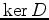 and
and
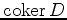 are representations of
are representations of 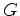 , and so
, and so
 is a virtual representation of
is a virtual representation of 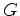 . We say that the operator
. We say that the operator
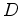 is rigid if its index is a multiple of the trivial
representation of dimension
is rigid if its index is a multiple of the trivial
representation of dimension 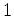 . The rigidity of
. The rigidity of 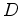 means that any
nontrivial irreducible representation of
means that any
nontrivial irreducible representation of 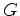 in
in 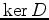 occurs in
occurs in
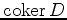 with the same multiplicity and vice versa.
with the same multiplicity and vice versa.
If the multiple 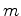 is positive, then
is positive, then
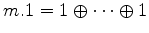 is
the trivial representation of dimension of
is
the trivial representation of dimension of 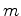 . If
. If 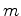 is negative, the
is negative, the
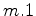 is a virtual representation and the rigidity of
is a virtual representation and the rigidity of 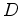 implies that the
trivial representation
implies that the
trivial representation 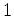 occurs more often in
occurs more often in
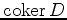 than in
than in 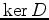 .
.
For a circle action on a compact oriented Riemannian manifold, it is well
known that the Hodge operator
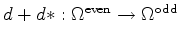 and the signature operator
and the signature operator
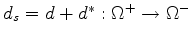 are both rigid.
are both rigid.
An oriented Riemannian manifold of dimension 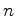 has an atlas whose transition
functions take values in
has an atlas whose transition
functions take values in
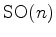 . The manifold is called a spin
manifold if it is possible to lift the transition functions to the double cover
. The manifold is called a spin
manifold if it is possible to lift the transition functions to the double cover
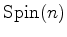 of
of
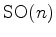 .
.
Inspired by physics, Witten discovered infinitely many rigid elliptic
operators on a compact spin manifold with a circle action.
They are typically of the form
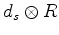 , where
, where 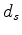 is the signature operator
and
is the signature operator
and 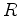 is some combination of the exterior and the symmetric powers of
the tangent bundle. In [91] Bott and Taubes
found a proof, more accessible to mathematicians, of Witten's results, by
recasting the rigidity theorem as a consequence of
the Atiyah-Bott fixed point theorem.
is some combination of the exterior and the symmetric powers of
the tangent bundle. In [91] Bott and Taubes
found a proof, more accessible to mathematicians, of Witten's results, by
recasting the rigidity theorem as a consequence of
the Atiyah-Bott fixed point theorem.
The idea of [91] is as follows. To decompose a representation, one needs
to know only its trace, since the trace determines the representation.
By assumption, the action of 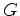 on the elliptic complex
on the elliptic complex
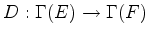 commutes with
commutes with 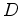 . This means each element
. This means each element 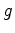 in
in 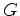 is an
endomorphism of the elliptic complex. It therefore induces an
endomorphism
is an
endomorphism of the elliptic complex. It therefore induces an
endomorphism 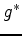 in the cohomology of the complex. But
in the cohomology of the complex. But
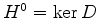 and
and
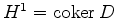 . The alternating sum of the trace of
. The alternating sum of the trace of 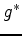 in cohomology
is precisely the left-hand side of the Atiyah-Bott fixed point theorem.
It then stands to reason that the fixed point theorem could be used to
decompose the index of
in cohomology
is precisely the left-hand side of the Atiyah-Bott fixed point theorem.
It then stands to reason that the fixed point theorem could be used to
decompose the index of 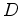 into irreducible representations.
into irreducible representations.
Papers of Raoul Bott discussed in this article
- [1]
- (with R. J. Duffin) Impedance synthesis without use of
transformers, J. Appl. Phys., 20 (1949), 816.
- [8]
- On torsion in Lie groups, Proc. NAS, 40 (1954), 586-588.
- [9]
- Nondegenerate critical manifolds, Ann. of Math. 60
(1954), 248-261.
- [12]
- (with H. Samelson) The cohomology ring of
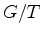 ,
Proc. NAS, 41 (1955), 490-493.
,
Proc. NAS, 41 (1955), 490-493.
- [14]
- On the iteration of closed geodesics and the Sturm
Intersection theory, Comm. Pure Appl. Math. IX (1956), 171-206.
- [15]
- Homogeneous vector bundles, Ann. of Math. 66 (1957),
933-935.
- [24]
- The stable homotopy of the classical groups, Ann. of Math.
70 (1959), 313-337.
- [33]
- (with M. F. Atiyah and A. Shapiro) Clifford modules,
Topology 3 (1965), 3-38.
- [37]
- The index theorem for homogeneous differential operators, in:
Differential and Combinatorial Topology: A Symposium in Honor of
Marston Morse, Princeton, (1964), 167-186.
- [38]
- (with S. Chern) Hermitian vector bundles and the
equidistribution of the zeroes of their holomorphic sections, Acta
Mathematics 114 (1964), 71-112.
- [41]
- Vector fields and characteristic numbers, Mich. Math.
Jour. 14 (1967), 231-244.
- [42]
- (with M. F. Atiyah) A Lefschetz fixed point formula for
elliptic complexes: I, Ann. of Math. 86 (1967), 374-407.
- [43]
- A residue formula for holomorphic vector fields, J.
Differential Geom. 1 (1967), 311-330.
- [44]
- (with M. F. Atiyah) A Lefschetz fixed point formula for
elliptic complexes: II, Ann. of Math. 88 (1968), 451-491.
- [51]
- On a topological obstruction to integrability, in: Global Analysis, Proceedings of Symposia in Pure Math. XVI (1970),
127-131.
- [71]
- (with G. Segal) The cohomology of the vector fields on a
manifold, Topology 16 (1977), 285-298.
- [81]
- (with M. F. Atiyah) The Yang-Mills equations over Riemann
surfaces, Phil. Trans. R. Soc. Lond. A 308 (1982), 524-615.
- [82]
- (with M. F. Atiyah) The moment map and equivariant
cohomology, Topology 23 (1984), 1-28.
- [91]
- (with C. Taubes) On the rigidity theorem of Witten,
Jour. of the Amer. Math.
Soc. 2 (1989), 137-186.
Update to the Bibliography of Raoul Bott
Raoul Bott's Bibliography in his Collected Papers [B5]
is not complete.
This update completes the Bibliography as of June 2000.
- [20]
- In memoriam Sumner B. Myers, Mich. Math. Jour., 5 (1958),
1-4.
- [79]
- (with L. Tu) Differential Forms in Algebraic Topology,
Springer-Verlag, (1982), 1-331.
- [94]
- Georges de Rham: 1901-1990, Notices Amer. Math. Soc.
38 (1991), 114-115.
- [95]
- Stable bundles revisited, Surveys in Differential Geometry,
1 (1991), 1-18.
- [96]
- On E. Verlinde's formula in the context of stable bundles,
Internat. J. Modern Phys. A 6 (1991), 2847-2858.
- [97]
- Nomination for Stephen Smale, Notices Amer. Math. Soc.,
38 (1991), 758-760..
- [98]
- On knot and manifold invariants, in: New Symmetry
Principles in Quantum Field Theory (Cargèse, 1991), NATO Adv. Sci.
Inst. Ser. B Phys. 295, Plenum, (1992),
37-52.
- [99]
- Topological aspects of loop groups, in: Topological
Quantum Field Theories and Geometry of Loop Spaces (Budapest, 1989),
World Sci. Publishing, (1992), 65-80.
- [100]
- For the Chern volume, in: Chern--a Great Geometer of the
Twentieth Century, Internat. Press, (1992), 106-108.
- [101]
- Reflections on the theme of the poster, in: Topological
Methods in Modern Mathematics (Stony Brook, NY, 1991), Publish or Perish
(1993), 125-135.
- [102]
- Luncheon talk and nomination for Stephen Smale, in: From Topology to Computation: Proceedings of the Smalefest (Berkeley, CA,
1990), Springer, (1993), 67-72.
- [103]
- (with C. Taubes) On the self-linking of knots, J. Math.
Phys. 35 (1994), 5247-5287.
- [104]
- On invariants of manifolds, in: Modern Methods in
Complex Analysis (Princeton, NJ, 1992), Ann. of Math. Stud., 137,
Princeton Univ. Press, (1995), 29-39.
- [105]
- Configuration spaces and imbedding invariants, Turkish J.
Math. 20 (1996), 1-17.
- [106]
- Configuration spaces and imbedding problems, in: Geometry and Physics (Aarhus, 1995), Lecture Notes in Pure and Appl.
Math., 184, Dekker (1997), 135-140.
- [107]
- Critical point theory in mathematics and in mathematical
physics, Turkish J. Math. 21 (1997), 9-40.
- [108]
- (with A. Cattaneo) Integral invariants of
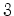 -manifolds, J.
Differential Geom. 48 (1998), 91-133.
-manifolds, J.
Differential Geom. 48 (1998), 91-133.
- [109]
- An introduction to equivariant cohomology, in: Quantum
Field Theory: Perspective and Prospective, Kluwer Academic Publishers,
(1999), 35-57.
- [110]
- (with A. Cattaneo) Integral invariants of
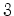 -manifolds,
II, to appear in J. Differential Geom.
-manifolds,
II, to appear in J. Differential Geom.


Next: Bibliography
Up: The life and works
Previous: Yang-Mills equations over Riemann
HTML generated on
2005-12-21
![]() and
and ![]() be vector bundles over a compact manifold
be vector bundles over a compact manifold ![]() . If a
differential operator
. If a
differential operator
![]() is elliptic, then
is elliptic, then
![]() and
and
![]() are finite-dimensional vector spaces and we can
define the index of
are finite-dimensional vector spaces and we can
define the index of ![]() to be the virtual vector space
to be the virtual vector space
![]() acts on
acts on ![]() , and
, and ![]() and
and ![]() are
are
![]() -equivariant vector bundles over
-equivariant vector bundles over ![]() . Then
. Then ![]() acts on
acts on
![]() by
by
![]() is positive, then
is positive, then
![]() is
the trivial representation of dimension of
is
the trivial representation of dimension of ![]() . If
. If ![]() is negative, the
is negative, the
![]() is a virtual representation and the rigidity of
is a virtual representation and the rigidity of ![]() implies that the
trivial representation
implies that the
trivial representation ![]() occurs more often in
occurs more often in
![]() than in
than in ![]() .
.
![]() and the signature operator
and the signature operator
![]() are both rigid.
are both rigid.
![]() has an atlas whose transition
functions take values in
has an atlas whose transition
functions take values in
![]() . The manifold is called a spin
manifold if it is possible to lift the transition functions to the double cover
. The manifold is called a spin
manifold if it is possible to lift the transition functions to the double cover
![]() of
of
![]() .
.
![]() , where
, where ![]() is the signature operator
and
is the signature operator
and ![]() is some combination of the exterior and the symmetric powers of
the tangent bundle. In [91] Bott and Taubes
found a proof, more accessible to mathematicians, of Witten's results, by
recasting the rigidity theorem as a consequence of
the Atiyah-Bott fixed point theorem.
is some combination of the exterior and the symmetric powers of
the tangent bundle. In [91] Bott and Taubes
found a proof, more accessible to mathematicians, of Witten's results, by
recasting the rigidity theorem as a consequence of
the Atiyah-Bott fixed point theorem.
![]() on the elliptic complex
on the elliptic complex
![]() commutes with
commutes with ![]() . This means each element
. This means each element ![]() in
in ![]() is an
endomorphism of the elliptic complex. It therefore induces an
endomorphism
is an
endomorphism of the elliptic complex. It therefore induces an
endomorphism ![]() in the cohomology of the complex. But
in the cohomology of the complex. But
![]() and
and
![]() . The alternating sum of the trace of
. The alternating sum of the trace of ![]() in cohomology
is precisely the left-hand side of the Atiyah-Bott fixed point theorem.
It then stands to reason that the fixed point theorem could be used to
decompose the index of
in cohomology
is precisely the left-hand side of the Atiyah-Bott fixed point theorem.
It then stands to reason that the fixed point theorem could be used to
decompose the index of ![]() into irreducible representations.
into irreducible representations.