Index of a closed geodesic

For two points $p$ and $q$ on a Riemannian manifold $M$ , the space $\Omega_{p,q}(M)$ of all paths from $p$ to $q$ on $M$ is not a finite-dimensional manifold. Nonetheless, Morse theory applies to this situation also, with a Morse function on the path space $\Omega_{p,q}$ given by the energy of a path:

$$E(\mu )=\int_a^b \langle \frac{d\mu}{dt}, \frac{d\mu}{dt} \rangle dt.$$

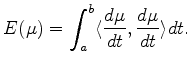
The first result of this infinite-dimensional Morse theory asserts that the critical points of the energy function are precisely the geodesics from $p$ to $q$ .

Two points $p$ and $q$ on a geodesic are conjugate if keeping $p$ and $q$ fixed, one can vary the geodesic from $p$ to $q$ through a family of geodesics. For example, two antipodal points on an $n$ -sphere are conjugate points. The multiplicity of $q$ as a conjugate point of $p$ is the dimension of the family of geodesics from $p$ to $q$ . On the $n$ -sphere $S^n$ , the multiplicity of the south pole as a conjugate point of the north pole is therefore $n-1$ .

If $p$ and $q$ are not conjugate along the geodesic, then the geodesic is nondegenerate as a critical point of the energy function on $\Omega_{p,q}$ . Its index, according to the Morse index theorem, is the number of conjugate points from $p$ to $q$ counted with multiplicities.

Figure 6: Geodesics on a sphere

On the $n$ -sphere let $p$ and $p'$ be antipodal points and $q \ne p'$ . The geodesics from $p$ to $q$ are $pq, pp'q, pqp'pq, pp'qpp'q, \dots$ , of index $0, n-1, 2(n-1), 3(n-1), \dots$ , respectively. By the Morse index theorem the energy function on the path space $\Omega_{p,q}(S^n)$ has one critical point each of index $0, n-1, 2(n-1), 3(n-1), \dots$ . It then follows from Morse theory that $\Omega_{p,q}(S^n)$ has the homotopy type of a CW complex with one cell in each of the dimensions $0, n-1, 2(n-1), 3(n-1), \dots$ .

Now consider the space $\Omega M$ of all smooth loops in $M$ , that is, smooth functions $\mu: S^1 \to M$ . The critical points of the energy function on $\Omega M$ are again the geodesics, but these are now closed geodesics. A closed geodesic is never isolated as a critical point, since for any rotation $r: S^1 \to S^1$ of the circle, $\mu \mathrel{\scriptstyle\circ}r: S^1 \to M$ is still a geodesic. In this way, any closed geodesic gives rise to a circle of closed geodesics. When the Riemannian metric on $M$ is generic, the critical manifolds of the energy function on the loop space $\Omega$ will all be circles.

Morse had shown that the index of a geodesic is the number of negative eigenvalues of a Sturm differential equation, a boundary-value problem of the form $Ly=\lambda y$ , where $L$ is a self-adjoint second-order differential operator. For certain boundary conditions, Morse had expressed the index in terms of conjugate points, but this procedure does not apply to closed geodesics, which correspond to a Sturm problem with periodic boundary conditions.

In [14] Bott found an algorithm to compute the index of a closed geodesic. He was then able to determine the behavior of the index when the closed geodesic is iterated. Bott's method is in fact applicable to all Sturm differential equations. And so in his paper he also gave a geometric formulation and new proofs of the Sturm-Morse separation, comparison, and oscillation theorems, all based on the principle that the intersection number of two cycles of complementary dimensions is zero if one of the cycles is homologous to zero.