In the Fifties Bott applied Morse theory with great success to the topology
of Lie groups and homogeneous spaces.
In [8] he showed how the diagram of a compact semisimple
connected and simply connected group ![]() determines the integral homology
of both the loop space
determines the integral homology
of both the loop space ![]() and the flag manifold
and the flag manifold ![]() , where
, where ![]() is a maximal torus.
is a maximal torus.
Indeed, Morse theory gives a beautiful CW cell structure on ![]() , up to
homotopy equivalence. To
explain this, recall that the adjoint action of the group
, up to
homotopy equivalence. To
explain this, recall that the adjoint action of the group ![]() on its Lie
algebra
on its Lie
algebra
![]() restricts to an action of the maximal torus
restricts to an action of the maximal torus ![]() on
on
![]() . As
a representation of the torus
. As
a representation of the torus ![]() , the Lie algebra
, the Lie algebra
![]() decomposes into a
direct sum of irreducible representations
decomposes into a
direct sum of irreducible representations
where
For example, for the group
![]() and maximal torus
and maximal torus
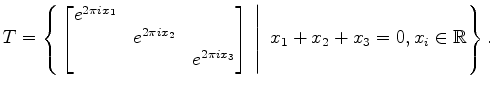
the roots are
For
![]() and
and
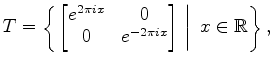
the Lie algebra
A point ![]() in
in
![]() is regular if its normalizer has minimal
possible dimension, or equivalently, if its normalizer is
is regular if its normalizer has minimal
possible dimension, or equivalently, if its normalizer is ![]() . It is well
known that a point
. It is well
known that a point ![]() in
in
![]() is regular if and only if it does not lie
on any of the hyperplanes of the diagram. If
is regular if and only if it does not lie
on any of the hyperplanes of the diagram. If ![]() is regular, then the
stabilizer of
is regular, then the
stabilizer of ![]() under the adjoint action of
under the adjoint action of ![]() is
is ![]() and so the orbit
through
and so the orbit
through ![]() is
is ![]() .
.
Choose another regular point ![]() in
in
![]() and define the function
and define the function ![]() on
on
![]() to be the distance from
to be the distance from ![]() ; here the distance is
measured with respect to the Killing form on
; here the distance is
measured with respect to the Killing form on
![]() .
Let
.
Let ![]() be all
the points in
be all
the points in
![]() obtained from
obtained from ![]() by reflecting about the root
planes. Then Bott's theorem asserts that
by reflecting about the root
planes. Then Bott's theorem asserts that ![]() is a Morse function on
is a Morse function on ![]() whose critical points are precisely all the
whose critical points are precisely all the ![]() 's. Moreover, the index
of a critical point
's. Moreover, the index
of a critical point ![]() is twice the number of times that the line
segment from
is twice the number of times that the line
segment from ![]() to
to ![]() intersects the root planes. This cell
decomposition of Morse theory fits in with the more group-theoretic Bruhat
decomposition.
intersects the root planes. This cell
decomposition of Morse theory fits in with the more group-theoretic Bruhat
decomposition.
For
![]() and
and ![]() the set of diagonal matrices in
the set of diagonal matrices in
![]() , the
orbit
, the
orbit ![]() is the complex flag manifold
is the complex flag manifold
![]() , consisting of all
flags
, consisting of all
flags
Bott's recipe gives 6 critical points of index