The periodicity theorem

Homotopy groups are notoriously difficult to compute. For a simple space like the $n$ -sphere, already, the higher homotopy groups exhibits no discernible patterns. It was therefore a complete surprise in 1957, when Raoul Bott computed the stable homotopy groups of the classical groups and found a simple periodic pattern for each of the classical groups [24].

We first explain what is meant by the stable homotopy group. Consider the unitary group $U(n+1)$ . It acts transitively on the unit sphere $S^{2n+1}$ in $\mathbb{C}^{n+1}$ , with stabilizer $U(n)$ at the point $(1,0,\dots,0)$ . In this way, the sphere $S^{2n+1}$ can be identified with the homogeneous space $U(n+1)/U(n)$ , and there is a fibering $U(n+1) \to S^{2n+1}$ with fiber $U(n)$ . By the homotopy exact sequence of a fibering, the following sequence is exact:

$$\dots \to \pi_{k+1}(S^{2n+1}) \to \pi_k (U(n)) \to \pi_k (U(n+1)) \to \pi_k (S^{2n+1}) \to \dots.$$

Since $\pi_k (S^m) = 0$ for $m > k$ , it follows immediately that as $n$ goes to infinity (in fact for all $n > k/2$ ), the $k$ th homotopy group of the unitary group stabilizes:

$$\pi_k (U(n)) = \pi_k (U(n+1)) = \pi_k(U(n+2)) = \dots.$$

This common value is called the $k$ th stable homotopy group of the unitary group, denoted $\pi_k (U)$ .

In the original proof of the periodicity theorem [24], Bott showed that in the loop space of the special unitary group $\operatorname{SU}(2n)$ , the manifold of minimal geodesics is the complex Grassmannian

$$G(n,2n) =\frac{U(2n)}{U(n)\times U(n)}.$$

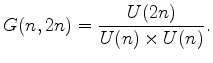
By Morse theory, the loop space $\Omega \operatorname{SU}(2n)$ has the homotopy type of a CW complex obtained from the Grassmannian $G(n,2n)$ by attaching cells of dimension $\ge 2n+2$ :

$$\Omega \operatorname{SU}(2n) \sim G(n,2n) \cup e_{\lambda} \cup \dots, \quad\dim e_{\lambda} \ge 2n+2.$$

It follows that

$$\pi_k (\Omega \operatorname{SU}(2n)) = \pi_k (G(n,2n))$$

for $n >> k$ .

It is easily shown that

$$\pi_k (\Omega \operatorname{SU}(2n)) = \pi_{k+1}(\operatorname{SU}(2n)) = \pi_{k+1}(U(2n)).$$

Using the homotopy exact sequence of the fibering

$$U(n) \to U(2n)/U(n) \to G(n,2n),$$

one gets

$$\pi_k (G(n,2n)) = \pi_{k-1} (U(n)).$$

Putting all this together, for $n$ large relative to $k$ , we get

$$\pi_{k-1} (U(n)) = \pi_k (G(n,2n)) = \pi_k(\Omega\operatorname{SU}(2n)) = \pi_{k+1}(U(2n)).$$

Thus, the stable homotopy group of the unitary group is periodic of period $2$ :

$$\pi_{k-1} (U) = \pi_{k+1} (U).$$

Applying the same method to the orthogonal group and the symplectic group, Bott showed that their stable homotopy groups are periodic of period $8$ .