The Clifford algebra ![]() is the algebra over
is the algebra over
![]() with
with ![]() generators
generators
![]() and relations
and relations
The first few Clifford algebras are easy to describe
If
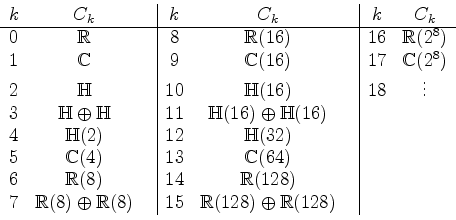
This table exhibits clearly a periodic pattern of period ![]() ,
except for the dimension increase after each period.
The
,
except for the dimension increase after each period.
The ![]() -fold periodicity of the Clifford algebras, long known to
algebraists, is reminiscent of the
-fold periodicity of the Clifford algebras, long known to
algebraists, is reminiscent of the ![]() -fold
periodicity of the stable homotopy groups of the orthogonal group.
-fold
periodicity of the stable homotopy groups of the orthogonal group.
In the early Sixties Michael Atiyah, Raoul Bott, and Arnold Shapiro found an explanation for this tantalizing connection. The link is provided by a class of linear differential operators called the Dirac operators. The link between differential equations and homotopy groups first came about as a result of the realization that ellipticity of a differential operator can be defined in terms of the symbol of the differential operator.
Suppose we can find ![]() real matrices
real matrices
![]() of size
of size
![]() satisfying
satisfying
This corresponds to a real representation of the Clifford algebra
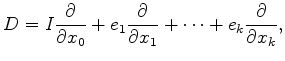
where
The Dirac operator
Since
The paper [33] shows that the minimal-dimensional representations of the
Clifford algebras give rise to Dirac operators whose symbols generate the
stable homotopy groups of the orthogonal group. In this way, the ![]() -fold
periodicity of the Clifford algebras reappears as the
-fold
periodicity of the Clifford algebras reappears as the ![]() -fold periodicity
of the stable homotopy groups of the orthogonal group.
-fold periodicity
of the stable homotopy groups of the orthogonal group.