Nevanlinna theory and the Bott-Chern classes

Nevanlinna theory deals with the following type of questions: Let $f:\mathbb{C} \to \mathbb{C}P^1$ be a holomorphic map. Given $a$ in $\mathbb{C}P^1$ , what is the inverse image $f^{-1}(a)$ ? Since $\mathbb{C}$ is noncompact, there may be infinitely many points in the pre-image $f^{-1}(a)$ . Sometimes $f^{-1}(a)$ will be empty, meaning that $f$ misses the point $a$ in $\mathbb{C}P^1$ .

The exponential map $\exp : \mathbb{C}\to \mathbb{C}P^1$ misses exactly two points, 0 and $\infty$ , in $\mathbb{C}P^1$ . According to a classical theorem of Picard, a nonconstant holomorphic map $f:\mathbb{C} \to \mathbb{C}P^1$ cannot miss more than two points.

Nevanlinna theory refines Picard's theorem in a beautiful way. To each $a \in \mathbb{C}P^1$ , it attaches a real number $\delta (a)$ between 0 and $1$ inclusive, the deficiency index of $a$ . The deficiency index is a normalized way of counting the number of points in the inverse image. If $f^{-1}(a)$ is empty, then the deficiency index is $1$ .

In this context the first main theorem of Nevanlinna theory says that a nonconstant holomorphic map $f:\mathbb{C} \to \mathbb{C}P^1$ has deficiency index 0 almost everywhere. The second main theorem yields the stronger inequality:

$$\sum_{a\in \mathbb{C}P^1} \delta (a) \le 2.$$

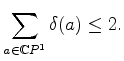
Ahlfors generalized these two theorems to holomorphic maps with values in a complex projective space $\mathbb{C}P^n$ .

In [38] Bott and Chern souped up Nevanlinna's hard analysis to give a more conceptual proof of the first main theorem.

A by-product of Bott and Chern's excursion in Nevanlinna theory is the notion of a refined Chern class, now called the Bott-Chern class, that has since been transformed into a powerful tool in Arakelov geometry and other aspects of modern number theory.

Briefly, the Bott-Chern classes arise as follows. On a complex manifold $M$ the exterior derivative $d$ decomposes into a sum $d= \partial + \bar{\partial}$ , and the smooth $k$ -forms decompose into a direct sum of $(p,q)$ -forms. Let $A^{p,p}$ be the space of smooth $(p,p)$ -forms on $M$ . Then the operator $\partial \bar{\partial}$ makes $\oplus A^{p,p}$ into a differential complex. Thus, the cohomology $H^*\{ A^{p,p}, \partial \bar{\partial} \}$ is defined.

A Hermitian structure on a holomorphic rank $n$ vector bundle $E$ on $M$ determines a unique connection and hence a unique curvature tensor. If $K$ and $K'$ are the curvature forms determined by two Hermitian structures on $E$ and $\phi$ is a $\operatorname{GL}(n,\mathbb{C})$ -invariant polynomial on $\mathfrak{gl}(n,\mathbb{C})$ , then it is well known that $\phi (K)$ and $\phi(K')$ are global closed forms on $M$ whose difference is exact:

$$\phi (K) - \phi(K') = d \alpha$$

for a differential form $\alpha$ on $M$ . This allows one to define the characteristic classes of $E$ as cohomology classes in $H^*(M)$ .

In the holomorphic case, $\phi (K)$ and $\phi(K')$ are $(p,p)$ -forms closed under $\partial \bar{\partial}$ . Bott and Chern found that in fact,

$$\phi (K) - \phi(K') = \partial \bar{\partial} \beta$$

for some $(p-1,p-1)$ -form $\beta$ . For a holomorphic vector bundle $E$ , the Bott-Chern class of $E$ associated to an invariant polynomial $\phi$ is the cohomology class of $\phi (E)$ , not in the usual cohomology, but in the cohomology of the complex $\{ A^{p,p}, \partial \bar{\partial} \}$ .