According to the celebrated Hopf index theorem, the Euler characteristic of a smooth manifold is equal to the number of zeros of a vector field on the manifold, each counted with its index. In [41] and [43], Bott generalized the Hopf index theorem to other characteristic numbers such as the Pontryagin numbers of a real manifold and the Chern numbers of a complex manifold.
We will describe Bott's formula only for Chern numbers. Let ![]() be a
compact complex manifold of dimension
be a
compact complex manifold of dimension ![]() , and
, and
![]() the
Chern classes of the tangent bundle of
the
Chern classes of the tangent bundle of ![]() . The Chern numbers of
. The Chern numbers of ![]() are
the integrals
are
the integrals
![]() , as
, as ![]() ranges
over all weighted homogeneous polynomials of degree
ranges
over all weighted homogeneous polynomials of degree ![]() . Like the Hopf
index theorem, Bott's formula computes a Chern number in terms of the zeros
of a vector field
. Like the Hopf
index theorem, Bott's formula computes a Chern number in terms of the zeros
of a vector field ![]() on
on ![]() , but the vector field must be holomorphic and the
counting of the zeros is a little more subtle.
, but the vector field must be holomorphic and the
counting of the zeros is a little more subtle.
For any vector field ![]() and any
and any
![]() function
function ![]() on
on ![]() , the Lie
derivative
, the Lie
derivative
![]() satisfies:
satisfies:
It follows that at a zero
Thus, at
of the tangent space of
For any endomorphism ![]() of a vector space
of a vector space ![]() , we define the numbers
, we define the numbers
![]() to be the coefficients of its characteristic polynomial:
to be the coefficients of its characteristic polynomial:
Bott's Chern number formula is as follows. Let ![]() be a compact complex
manifold of complex dimension
be a compact complex
manifold of complex dimension ![]() and
and ![]() a holomorphic vector field having
only isolated nondegenerate zeros on
a holomorphic vector field having
only isolated nondegenerate zeros on ![]() . For any weighted homogeneous
polynomial
. For any weighted homogeneous
polynomial
![]() ,
,
![]() ,
,
In Bott's formula, if the polynomial ![]() does not have degree
does not have degree ![]() , then
the left-hand side of (2) is zero, and the formula
gives an identity among the numbers
, then
the left-hand side of (2) is zero, and the formula
gives an identity among the numbers ![]() . For the polynomial
. For the polynomial
![]() , Bott's formula recovers the Hopf index theorem:
, Bott's formula recovers the Hopf index theorem:
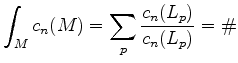 zeros of
zeros of
Bott's formula (2) is reminiscent of Cauchy's residue
formula and so the right-hand side of (2) may be viewed
as a residue of ![]() at
at ![]() .
.
In [43] Bott generalized his Chern number formula (2), which assumes isolated zeros, to holomorphic vector fields with higher-dimensional zero sets and to bundles other than the tangent bundle (a vector field is a section of the tangent bundle).