A continuous map of a finite polyhedron, ![]() , has a
Lefschetz number:
, has a
Lefschetz number:
where
In the smooth category the Lefschetz fixed point theorem has a quantitative
refinement. A smooth map ![]() from a compact manifold to itself is
transversal if its graph is transversal to the diagonal
from a compact manifold to itself is
transversal if its graph is transversal to the diagonal ![]() in
in
![]() . Analytically,
. Analytically, ![]() is transversal if and only if at each
fixed point
is transversal if and only if at each
fixed point ![]() ,
,
where
The
![]() Lefschetz fixed point theorem states that the Lefschetz
number of a transversal map
Lefschetz fixed point theorem states that the Lefschetz
number of a transversal map ![]() is the number of fixed points
is the number of fixed points ![]() counted
with multiplicity
counted
with multiplicity ![]() depending on the sign of the determinant
depending on the sign of the determinant
![]() :
:
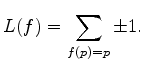
In the Sixties Atiyah and Bott proved a far-reaching generalization of the Lefschetz fixed point theorem ([42], [44]). This type of result, relating a global invariant to a sum of local contributions, is a recurring theme in some of Bott's best work.
To explain it, recall that the real singular cohomology of ![]() is
computable from the de Rham complex
is
computable from the de Rham complex
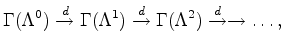
where
Let ![]() and
and ![]() be vector bundles of ranks
be vector bundles of ranks ![]() and
and ![]() respectively
over
respectively
over ![]() . An
. An
![]() -linear map
-linear map
is a differential operator if about every point in
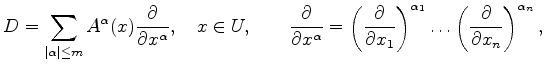
where
Given a cotangent vector
![]() , we write
, we write
and define the symbol of a differential operator
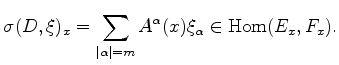
In other words, the symbol of
Let ![]() be vector bundles over a manifold
be vector bundles over a manifold ![]() . A differential complex
. A differential complex
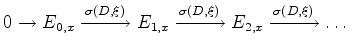
is an exact sequence of vector spaces.
A fundamental consequence of ellipticity is that all the cohomology spaces
![]() are finite-dimensional.
are finite-dimensional.
An endomorphism of the complex (3) is a collection of linear
maps
![]() such that
such that
for all
A map
![]() induces a natural map
induces a natural map
by composition:
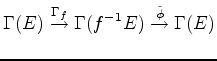
is an endomorphism of
In the case of the de Rham complex, a map ![]() induces a linear map
induces a linear map
![]() and hence a linear map
and hence a linear map
which is the lifting that finally defines the pullback of differential forms
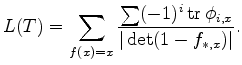
As evidence of its centrality, the Atiyah-Bott fixed point theorem has an astonishing range of applicability.
Here is an easily stated corollary in algebraic geometry: any holomorphic map of a rational algebraic manifold to itself has a fixed point.
Specializing the Atiyah-Bott fixed point theorem to the de Rham complex, one recovers the classical Lefschetz fixed point theorem. When applied to other geometrically interesting elliptic complexes, Atiyah and Bott obtained new fixed point theorems, such as a holomorphic Lefschetz fixed point theorem in the complex analytic case and a signature formula in the Riemannian case. In the homogeneous case, the fixed point theorem implies the Weyl character formula.