Localization in equivariant cohomology

Just as singular cohomology is a functor from the category of topological spaces to the category of rings, so when a group $G$ acts on a space $M$ , one seeks a functor that would incorporate both the topology of the space and the action of the group.

The naive construction of taking the cohomology of the quotient space $M/G$ is unsatisfactory because for a nonfree action, the topology of the quotient can be quite bad. A solution is to find a contractible space $EG$ on which $G$ acts freely, for then $EG \times M$ will have the same homotopy type as $M$ and the group $G$ will act freely on $EG \times M$ via the diagonal action. It is well known that such a space is the total space of the universal $G$ -bundle $EG\to BG$ , whose base space is the classifying space of $G$ . The homotopy theorists have defined the homotopy quotient $M_G$ of $M$ by $G$ to be the quotient space $(EG \times M)/G$ , and the equivariant cohomology $H_G^*(M)$ to be the ordinary cohomology of its homotopy quotient $M_G$ .

The equivariant cohomology of the simplest $G$ -space, a point, is already quite interesting, for it is the ordinary cohomology of the classifying space of $G$ :

$$H_G^*(\operatorname{pt})= H^*((EG\times \operatorname{pt})/G )= H^*(EG/G)= H^*(BG).$$

Since equivariant cohomology is a functor of $G$ -spaces, the constant map $M \to \operatorname{pt}$ induces a homomorphism $H_G^*(\operatorname{pt}) \to H_G^*(M)$ . Thus, the equivariant cohomology $H_G^*(M)$ has the structure of a module over $H^*(BG)$ .

Characteristic classes of vector bundles over $M$ extend to equivariant characteristic classes of equivariant vector bundles.

When $M$ is a manifold, there is a push-forward map $\pi_*^M: H_G^*(M) \to H_G^*(\operatorname{pt})$ , akin to integration along the fiber.

Suppose a torus $T$ acts on a compact manifold $M$ with fixed point set $F$ , and $\phi \in H_T^*(M)$ is an equivariantly closed class. Let $P$ be the connected components of $F$ and let $\iota_P:P\to M$ be the inclusion map, $\nu_P$ the normal bundle of $P$ in $M$ , and $e(\nu_P)$ the equivariant Euler class of $\nu_P$ . In [82] Atiyah and Bott proved a localization theorem for the equivariant cohomology $H_T^*(M)$ with real coefficients:

$$\pi_*^M \phi = \sum_P \pi_*^P \left( \dfrac{\iota_P^* \phi}{e(\nu_P)} \right).$$

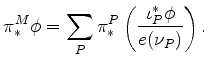
It should be noted that Berline and Vergne [BV] independently proved the same theorem at about the same time.

This localization theorem has as consequences the following results of Duistermaat and Heckman on a symplectic manifold $(M,\omega)$ of dimension of $2n$ :

1)

If a torus action on $M$ preserves the symplectic form and has a moment map $f$ , then the push-forward $f_{*} (\omega^n)$ of the symplectic volume under the moment map is piecewise polynomial.

2)

Under the same hypotheses, the stationary phase approximation for the integral

$$\int_M e^{-itf} \dfrac{\omega^n}{n!}$$

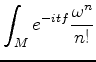
is exact.

In case the vector field on the manifold is generated by a circle action, the localization theorem specializes to Bott's Chern number formulas [41] of the Sixties, thus providing an alternative explanation for the Chern number formulas.