As mentioned earlier, the paper on impedance so impressed Hermann Weyl that he invited Bott to the Institute for Advanced Study at Princeton in 1949. There Bott came into contact with Marston Morse. Morse's theory of critical points would play a decisive role throughout Bott's career, notably in his work on homogeneous spaces, the Lefschetz hyperplane theorem, the periodicity theorem, and the Yang-Mills functional on a moduli space.
In the Twenties Morse had initiated the study of the critical points of
a function on a space and its relation to the topology of the space.
A smooth function ![]() on a smooth manifold
on a smooth manifold ![]() has a critical point
at
has a critical point
at ![]() in
in ![]() if there is a coordinate system
if there is a coordinate system
![]() at
at ![]() such that all the partial derivatives of
such that all the partial derivatives of ![]() vanish at
vanish at ![]() :
:
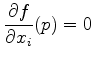 for all
for all Such a critical point is nondegenerate if the matrix of second partials, called the Hessian of
![$\displaystyle H_p f= \left[ \dfrac{\partial ^2 f}{\partial x_i \partial x_j}(p) \right],
$](img45.gif)
is nonsingular. The index
If a smooth function has only nondegenerate critical points, we call it a Morse function. The behavior of the critical points of a Morse function can be summarized in its Morse polynomial:
where the sum runs over all critical points
A typical example of a Morse function is
the height function ![]() of a torus standing
vertically on a table top (Figure 1).
of a torus standing
vertically on a table top (Figure 1).
The height function on this torus has four critical points of index 0, 1, 1, 2 respectively. Its Morse polynomial is
For a Morse function ![]() on a compact manifold
on a compact manifold ![]() , the fundamental results of
Morse theory hinge on the fact
that
, the fundamental results of
Morse theory hinge on the fact
that ![]() has the homotopy type of a CW complex with
one cell of dimension
has the homotopy type of a CW complex with
one cell of dimension ![]() for each critical point of
for each critical point of ![]() of index
of index
![]() .
This realization came about in the early Fifties, due to the work of
Pitcher, Thom, and Bott.
.
This realization came about in the early Fifties, due to the work of
Pitcher, Thom, and Bott.
Two consequences follow immediately:
If
is the Poincaré polynomial of
meaning that their difference
A Morse function ![]() on
on ![]() satisfying (1) is said to be
perfect. The height function on the torus above is a perfect Morse
function.
satisfying (1) is said to be
perfect. The height function on the torus above is a perfect Morse
function.
Classical Morse theory deals only with functions all of
whose critical points are nondegenerate; in particular, the critical
points must all be isolated points. In many situations, however, the
critical points form submanifolds of ![]() . For example, if the torus now
sits flat on the table, as a donut usually would, then the height function
has the top and bottom circles as critical manifolds
(Figure 2).
. For example, if the torus now
sits flat on the table, as a donut usually would, then the height function
has the top and bottom circles as critical manifolds
(Figure 2).
One of Bott's first insights was to see how to extend Morse theory to this
situation. In [9] he introduced the notion of a nondegenerate critical
manifold: a critical manifold ![]() is nondegenerate if at any point
is nondegenerate if at any point
![]() in
in ![]() the Hessian of
the Hessian of ![]() restricted to the normal space to
restricted to the normal space to ![]() is
nonsingular. The index
is
nonsingular. The index
![]() of the nondegenerate critical
manifold
of the nondegenerate critical
manifold ![]() is then defined to be the number of negative eigenvalues of
this normal Hessian; it represents the number of independent normal
directions along which
is then defined to be the number of negative eigenvalues of
this normal Hessian; it represents the number of independent normal
directions along which ![]() is decreasing.
For simplicity, assume that the normal bundles of the nondegenerate
critical manifolds are all orientable.
To form the Morse polynomial of
is decreasing.
For simplicity, assume that the normal bundles of the nondegenerate
critical manifolds are all orientable.
To form the Morse polynomial of
![]() , each critical manifold
, each critical manifold ![]() is counted with its Poincaré polynomial;
thus,
is counted with its Poincaré polynomial;
thus,
summed over all critical manifolds.
With this definition of the Morse polynomial, Bott proved in [9] that if a
smooth function ![]() on a smooth manifold
on a smooth manifold ![]() has only nondegenerate
critical manifolds, then the Morse inequality again holds:
has only nondegenerate
critical manifolds, then the Morse inequality again holds: